Spherical Harmonic Models 2#
# Import notebook dependencies
import sys
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
import numpy as np
import pandas as pd
from src import sha, lsfile, cfile, IGRF13_FILE
A more tangible example of modelling using spherical harmonics#
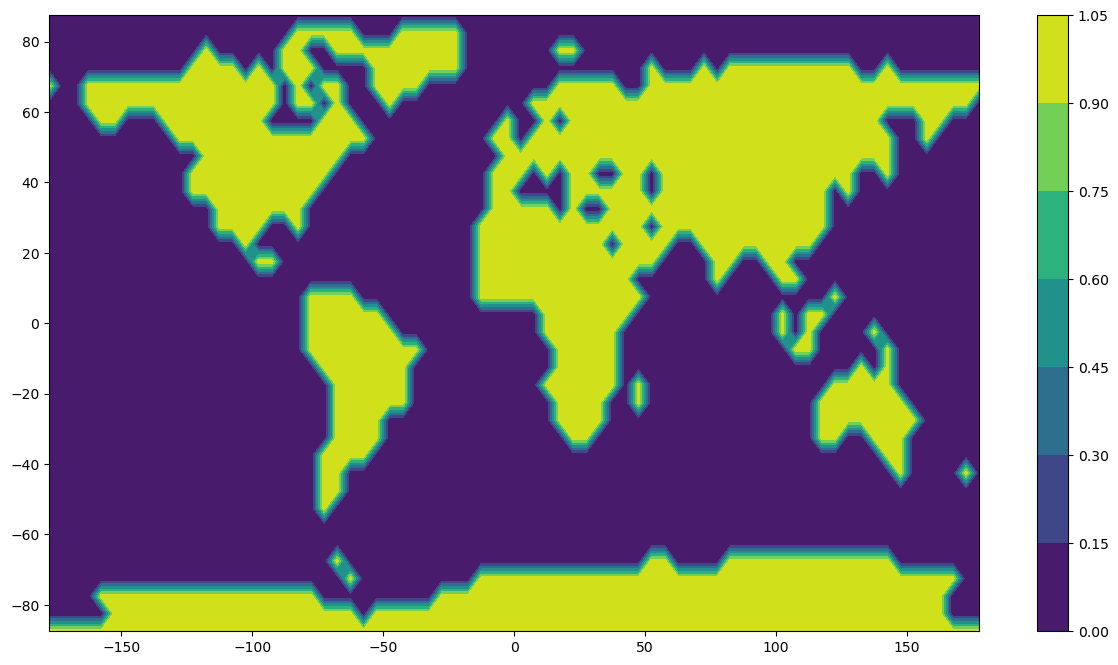
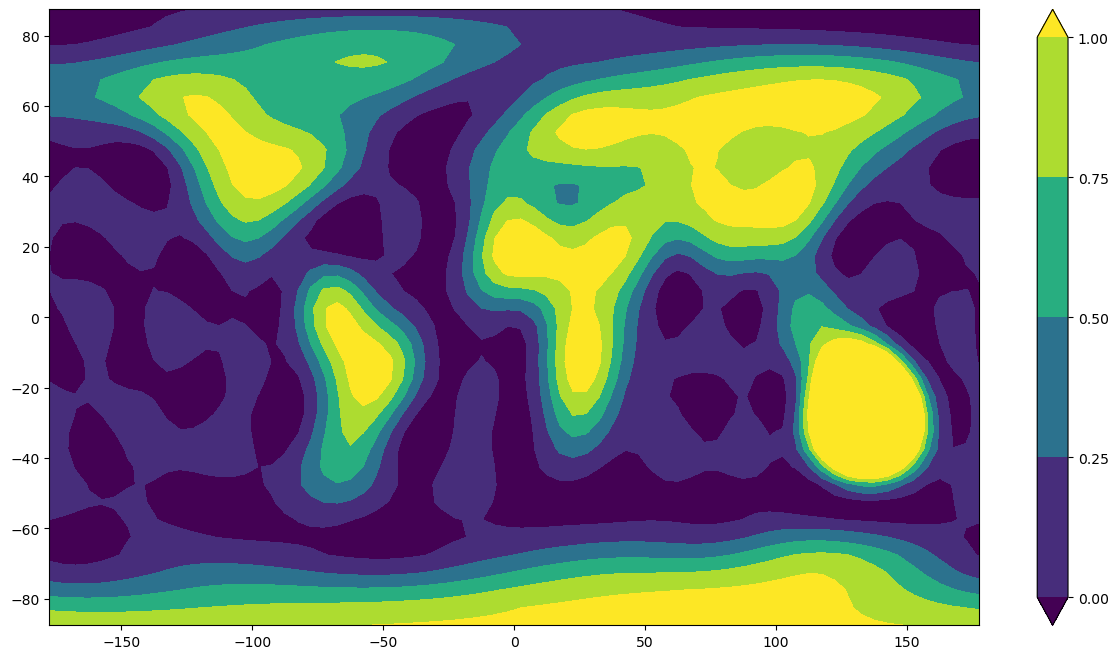
In this notebook we compute spherical harmonic models from an input data set representing a very simple world map with land encoded as 1 and water as 0 (so the data takes the values 0 and 1 only). We investigate the ability of models with different choices of maximum spherical harmonic degree to represent the data.
# Load the data
lsdata = np.genfromtxt(lsfile, delimiter=',')
x = lsdata[:,0].reshape(36, 72)
y = lsdata[:,1].reshape(36,72)
z = lsdata[:,2].reshape(36,72)
# Plot them
plt.rcParams['figure.figsize'] = [15, 8]
plt.contourf(x,y,z)
plt.colorbar()
plt.show()
>> USER INPUT HERE: Set the maximum spherical harmonic degree of the analysis
nmax = 10 # Max degree
# These functions are used for the spherical harmonic analysis and synthesis steps
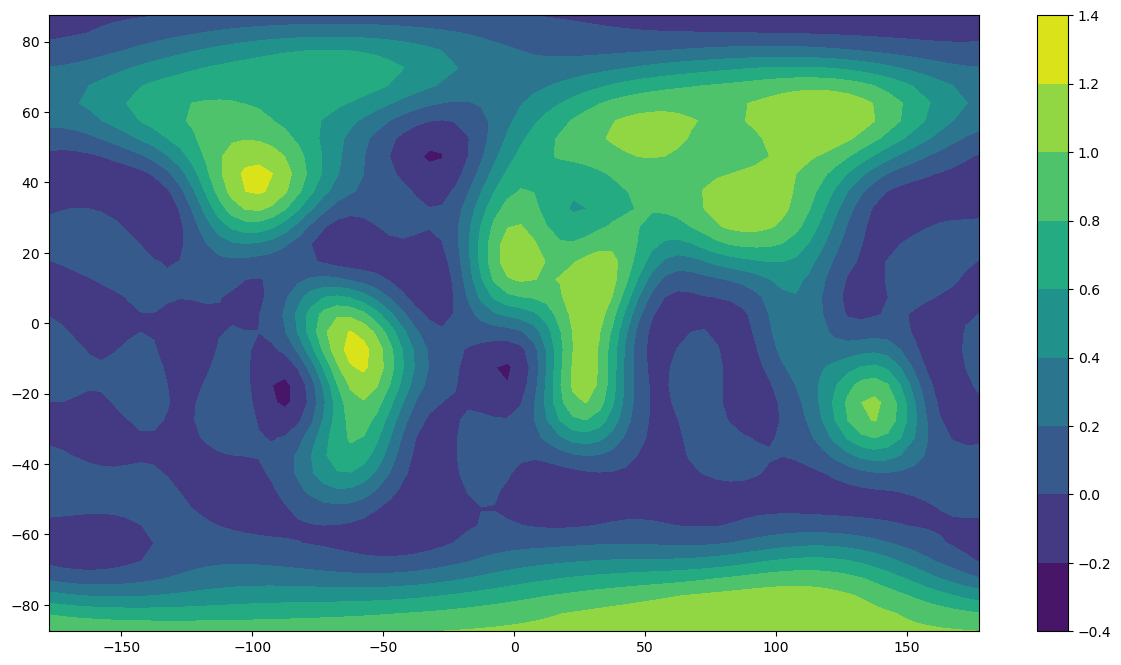
# Firstly compute a spherical harmonic model of degree and order nmax using the input data as plotted above
def sh_analysis(lsdata, nmax):
npar = (nmax+1)*(nmax+1)
ndat = len(lsdata)
lhs = np.zeros(npar*ndat).reshape(ndat,npar)
rhs = np.zeros(ndat)
line = np.zeros(npar)
ic = -1
for i in range(ndat):
th = 90 - lsdata[i][1]
ph = lsdata[i][0]
rhs[i] = lsdata[i][2]
cmphi, smphi = sha.csmphi(nmax,ph)
pnm = sha.pnm_calc(nmax, th)
for n in range(nmax+1):
igx = sha.gnmindex(n,0)
ipx = sha.pnmindex(n,0)
line[igx] = pnm[ipx]
for m in range(1,n+1):
igx = sha.gnmindex(n,m)
ihx = sha.hnmindex(n,m)
ipx = sha.pnmindex(n,m)
line[igx] = pnm[ipx]*cmphi[m]
line[ihx] = pnm[ipx]*smphi[m]
lhs[i,:] = line
shmod = np.linalg.lstsq(lhs, rhs.reshape(len(lsdata),1), rcond=None)
return(shmod)
# Now use the model to synthesise values on a 5 degree grid in latitude and longitude
def sh_synthesis(shcofs, nmax):
newdata =np.zeros(72*36*3).reshape(2592,3)
ic = 0
for ilat in range(36):
delta = 5*ilat+2.5
lat = 90 - delta
for iclt in range(72):
corr = 5*iclt+2.5
long = -180+corr
colat = 90-lat
cmphi, smphi = sha.csmphi(nmax,long)
vals = np.dot(sha.gh_phi(shcofs, nmax, cmphi, smphi), sha.pnm_calc(nmax, colat))
newdata[ic,0]=long
newdata[ic,1]=lat
newdata[ic,2]=vals
ic += 1
return(newdata)
# Obtain the spherical harmonic coefficients
shmod = sh_analysis(lsdata=lsdata, nmax=nmax)
# Read the model coefficients
shcofs = shmod[0]
# Synthesise the model coefficients on a 5 degree grid
newdata = sh_synthesis(shcofs=shcofs, nmax=nmax)
# Reshape for plotting purposes
x = newdata[:,0].reshape(36, 72)
y = newdata[:,1].reshape(36,72)
z = newdata[:,2].reshape(36,72)
# Plot the results
plt.rcParams['figure.figsize'] = [15, 8]
levels = [-1.5, -0.75, 0, 0.25, 0.5, 0.75, 2.]
plt.contourf(x,y,z)
plt.colorbar()
plt.show()
Spherical harmonic models with data gaps#
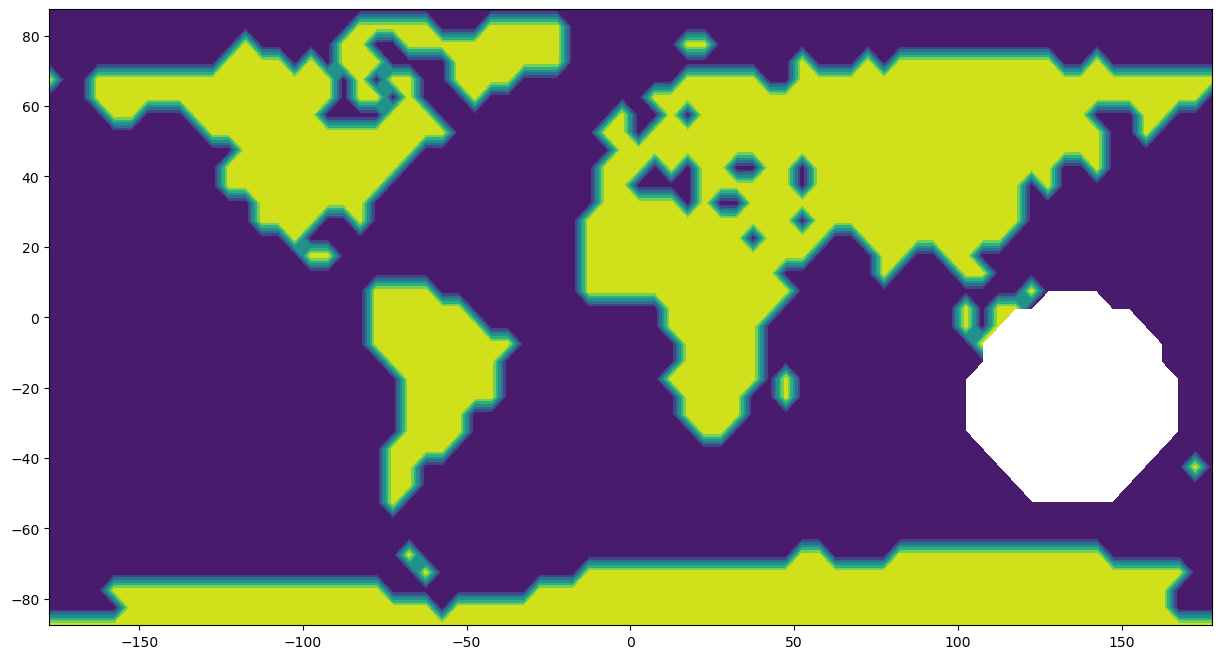
What happens if the data set is incomplete? In this section, you can experiment by removing data within a spherical cap of specified radius and pole position.
def greatcircle(th1, ph1, th2, ph2):
th1 = np.deg2rad(th1)
th2 = np.deg2rad(th2)
dph = np.deg2rad(dlong(ph1,ph2))
# Apply the cosine rule of spherical trigonometry
dth = np.arccos(np.cos(th1)*np.cos(th2) + \
np.sin(th1)*np.sin(th2)*np.cos(dph))
return(dth)
def dlong (ph1, ph2):
ph1 = np.sign(ph1)*abs(ph1)%360 # These lines return a number in the
ph2 = np.sign(ph2)*abs(ph2)%360 # range -360 to 360
if(ph1 < 0): ph1 = ph1 + 360 # Put the results in the range 0-360
if(ph2 < 0): ph2 = ph2 + 360
dph = max(ph1,ph2) - min(ph1,ph2) # So the answer is positive and in the
# range 0-360
if(dph > 180): dph = 360-dph # So the 'short route' is returned
return(dph)
def gh_phi(gh, nmax, cp, sp):
rx = np.zeros(nmax*(nmax+3)//2+1)
igx=-1
igh=-1
for i in range(nmax+1):
igx += 1
igh += 1
rx[igx]= gh[igh]
for j in range(1,i+1):
igh += 2
igx += 1
rx[igx] = (gh[igh-1]*cp[j] + gh[igh]*sp[j])
return(rx)
>> USER INPUT HERE: Set the location and size of the data gap
Enter the pole colatitude and longitude in degrees and the radius in km
# Remove a section of data centered on colat0, long0 and radius='radius':
colat0 = 113
long0 = 135
radius = 3000
lsdata_gap = lsdata.copy()
for row in range(len(lsdata_gap)):
colat = 90 - lsdata_gap[row,1]
long = lsdata_gap[row,0]
if greatcircle(colat, long, colat0, long0) < radius/6371.2:
lsdata_gap[row,2] = np.nan
print('Blanked out: ', np.count_nonzero(np.isnan(lsdata_gap)))
x_gap = lsdata_gap[:,0].reshape(36, 72)
y_gap = lsdata_gap[:,1].reshape(36,72)
z_gap = lsdata_gap[:,2].reshape(36,72)
# Plot the map with omitted data
plt.contourf(x_gap, y_gap, z_gap)
Blanked out: 104
<matplotlib.contour.QuadContourSet at 0x7fe3dc58f760>
USER INPUT HERE: Set the maximum spherical harmonic degree of the analysis
nmax = 12 #Max degree
# Select the non-nan data
lsdata_gap = lsdata_gap[~np.isnan(lsdata_gap[:,2])]
# Obtain the spherical harmonic coefficients for the incomplete data set
shmod = sh_analysis(lsdata=lsdata_gap, nmax=nmax)
# Read the model coefficients
shcofs = shmod[0]
# Synthesise the model coefficients on a 5 degree grid
newdata = sh_synthesis(shcofs=shcofs, nmax=nmax)
# Reshape for plotting purposes
x_new = newdata[:,0].reshape(36, 72)
y_new = newdata[:,1].reshape(36,72)
z_new = newdata[:,2].reshape(36,72)
Print the maximum and minimum of the synthesised data. How do they compare to the original data, which was composed of only ones and zeroes? How do the max/min change as you vary the data gap size and the analysis resolution? Why? Try this with a larger gap, e.g. 5000 km.
print(np.min(z_new))
print(np.max(z_new))
-0.25531903688873653
5.853211492921376
# Plot the results with colour scale according to the data
plt.rcParams['figure.figsize'] = [15, 8]
plt.contourf(x_new, y_new, z_new)
plt.colorbar()
plt.show()
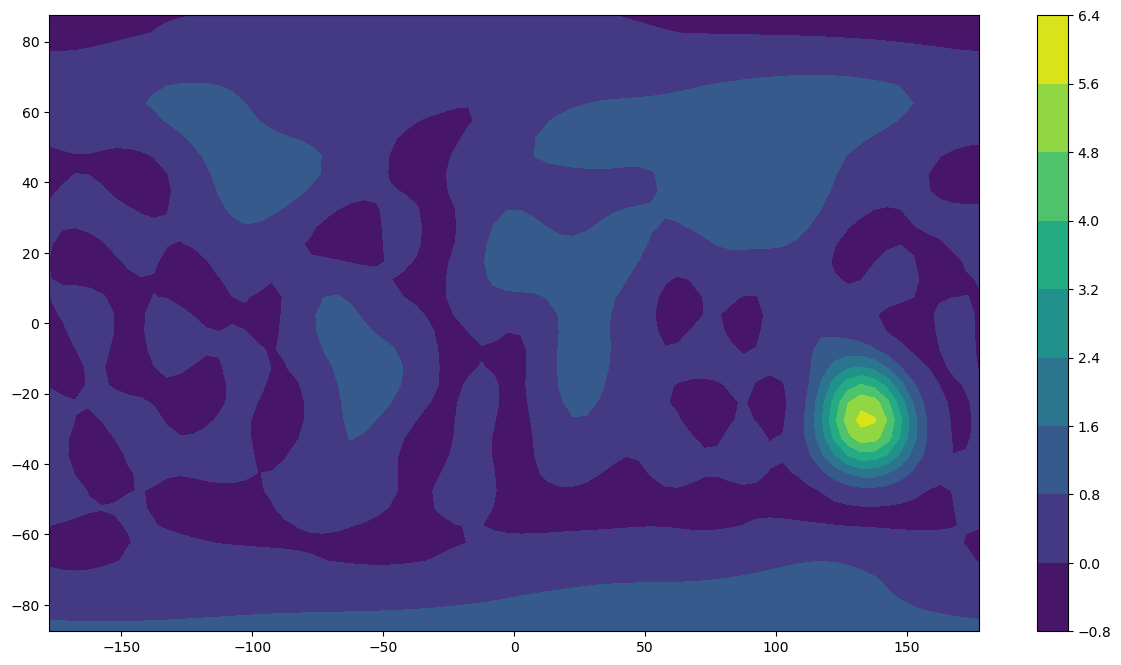
Now see what happens when we restrict the colour scale to values between 0 and 1 (so values <0 and >1 are compressed into opposite ends of the colour scale).
# Plot the results
plt.rcParams['figure.figsize'] = [15, 8]
levels = [0, 0.25, 0.5, 0.75, 1.]
plt.contourf(x_new, y_new, z_new, levels, extend='both')
plt.colorbar()
plt.show()
Making a spherical harmonic model of the geomagnetic field#
There is a file containing virtual observatory (VO) data calculated from the Swarm 3-satellite constellation in this repository. VOs use a local method to provide point estimates of the magnetic field at a specified time and fixed location at satellite altitude. This technique has various benefits, including:
Easier comparison between satellite (moving instrument) and ground observatory (fixed instrument) data, which is particularly useful when studying time changes of the magnetic field, e.g. geomagnetic jerks.
One can compute VOs on a regular spatial grid to mitigate the effects of uneven ground observatory coverage.
A brief summary of the method used to calculate each of these VO data points:
Swarm track data over four months are divided into 300 globally distributed equal area bins
Gross outliers (deviating over 500nT from the CHAOS-6-x7 internal field model) are removed
Only data from magnetically quiet, dark times are kept
Estimates of the core and crustal fields from CHAOS-6-x7 are subtracted from each datum to give the residuals
A local magnetic potential \(V\) is fit to the residuals within the cylinder
Values of the residual magnetic field in spherical coordinates (\(r\), \(\theta\), \(\phi\)) are computed from the obtained magnetic potential using \(B=-\nabla V\) at centre of the bin (at 490km altitude)
An estimate of the modelled core field at the VO calculation point is added back onto the residual field to give the total internal magnetic field value
In this section, we use VO data centred on 2015.0 to produce a degree 13 spherical harmonic model of the geomagnetic field and compare our (satellite data only) model to the IGRF (computed using both ground and satellite data) at 2015.0.
# Read in the VO data
cols = ['Year','Colat','Long','Rad','Br','Bt', 'Bp']
bvals = pd.read_csv(cfile, sep='\s+', skiprows=0, header=None, index_col=0,
na_values=[99999.00,99999.00000], names=cols, comment='%')
bvals = bvals.dropna()
bvals['Bt']= -bvals['Bt']
bvals['Br']= -bvals['Br']
colnames=['Colat','Long','Rad','Bt','Bp', 'Br']
bvals=bvals.reindex(columns=colnames)
bvals.columns = ['Colat','Long','Rad','X','Y','Z']
print(bvals.info())
# Set the date to 2015.0 (this is the only common date between the VO data file and the IGRF coefficients file)
epoch = 2015.0
# Set the model resolution to 13 (the same as IGRF)
nmax = 13
<class 'pandas.core.frame.DataFrame'>
Float64Index: 1444 entries, 2014.0 to 2018.0
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Colat 1444 non-null float64
1 Long 1444 non-null float64
2 Rad 1444 non-null float64
3 X 1444 non-null float64
4 Y 1444 non-null float64
5 Z 1444 non-null float64
dtypes: float64(6)
memory usage: 79.0 KB
None
def geomagnetic_model(epoch, nmax, data, RREF=6371.2):
# Select the data for that date
colat = np.array(data.loc[epoch]['Colat'])
nx = len(colat) # Number of data triples
ndat = 3*nx # Total number of data
elong = np.array(data.loc[epoch]['Long'])
rad = np.array(data.loc[epoch]['Rad'])
rhs = data.loc[epoch][['X', 'Y', 'Z']].values.reshape(ndat,1)
npar = (nmax+1)*(nmax+1) # Number of model parameters
nx = len(colat) # Number of data triples
ndat = 3*nx # Total number of data
print('Number of data triples selected =', nx)
# Arrays for the equations of condition
lhs = np.zeros(npar*ndat).reshape(ndat,npar)
linex = np.zeros(npar); liney = np.zeros(npar); linez = np.zeros(npar)
iln = 0 # Row counter
for i in range(nx): # Loop over data triplets (X, Y, Z)
r = rad[i]
th = colat[i]; ph = elong[i]
rpow = sha.rad_powers(nmax, RREF, r)
cmphi, smphi = sha.csmphi(nmax, ph)
pnm, xnm, ynm, znm = sha.pxyznm_calc(nmax, th)
for n in range(nmax+1): # m=0
igx = sha.gnmindex(n,0) # Index for g(n,0) in gh conventional order
ipx = sha.pnmindex(n,0) # Index for pnm(n,0) in array pnm
rfc = rpow[n]
linex[igx] = xnm[ipx]*rfc
liney[igx] = 0
linez[igx] = znm[ipx]*rfc
for m in range(1,n+1): # m>0
igx = sha.gnmindex(n,m) # Index for g(n,m)
ihx = igx + 1 # Index for h(n,m)
ipx = sha.pnmindex(n,m) # Index for pnm(n,m)
cpr = cmphi[m]*rfc
spr = smphi[m]*rfc
linex[igx] = xnm[ipx]*cpr; linex[ihx] = xnm[ipx]*spr
liney[igx] = ynm[ipx]*spr; liney[ihx] = -ynm[ipx]*cpr
linez[igx] = znm[ipx]*cpr; linez[ihx] = znm[ipx]*spr
lhs[iln, :] = linex
lhs[iln+1,:] = liney
lhs[iln+2 :] = linez
iln += 3
shmod = np.linalg.lstsq(lhs, rhs, rcond=None) # Include the monopole
# shmod = np.linalg.lstsq(lhs[:,1:], rhs, rcond=None) # Exclude the monopole
gh = shmod[0]
return(gh)
coeffs = geomagnetic_model(epoch=epoch, nmax=nmax, data=bvals)
Number of data triples selected = 299
Read in the IGRF coefficients for comparison
igrf13 = pd.read_csv(IGRF13_FILE, delim_whitespace=True, header=3)
igrf13.head()
| g/h | n | m | 1900.0 | 1905.0 | 1910.0 | 1915.0 | 1920.0 | 1925.0 | 1930.0 | ... | 1980.0 | 1985.0 | 1990.0 | 1995.0 | 2000.0 | 2005.0 | 2010.0 | 2015.0 | 2020.0 | 2020-25 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | g | 1 | 0 | -31543 | -31464 | -31354 | -31212 | -31060 | -30926 | -30805 | ... | -29992 | -29873 | -29775 | -29692 | -29619.4 | -29554.63 | -29496.57 | -29441.46 | -29404.8 | 5.7 |
| 1 | g | 1 | 1 | -2298 | -2298 | -2297 | -2306 | -2317 | -2318 | -2316 | ... | -1956 | -1905 | -1848 | -1784 | -1728.2 | -1669.05 | -1586.42 | -1501.77 | -1450.9 | 7.4 |
| 2 | h | 1 | 1 | 5922 | 5909 | 5898 | 5875 | 5845 | 5817 | 5808 | ... | 5604 | 5500 | 5406 | 5306 | 5186.1 | 5077.99 | 4944.26 | 4795.99 | 4652.5 | -25.9 |
| 3 | g | 2 | 0 | -677 | -728 | -769 | -802 | -839 | -893 | -951 | ... | -1997 | -2072 | -2131 | -2200 | -2267.7 | -2337.24 | -2396.06 | -2445.88 | -2499.6 | -11.0 |
| 4 | g | 2 | 1 | 2905 | 2928 | 2948 | 2956 | 2959 | 2969 | 2980 | ... | 3027 | 3044 | 3059 | 3070 | 3068.4 | 3047.69 | 3026.34 | 3012.20 | 2982.0 | -7.0 |
5 rows × 29 columns
# Select the 2015 IGRF coefficients
igrf = np.array(igrf13[str(epoch)])
# Insert a zero in place of the monopole coefficient (this term is NOT included in the IRGF, or any other field model)
igrf = np.insert(igrf, 0, 0)
Compare our model coefficients to IGRF13
print("VO only model \t IGRF13")
for i in range(196):
print("% 9.1f\t%9.1f" %(coeffs[i], igrf[i]))
VO only model IGRF13
-0.3 0.0
-29441.9 -29441.5
-1502.9 -1501.8
4784.9 4796.0
-2444.7 -2445.9
3012.8 3012.2
-2826.6 -2845.4
1676.4 1676.3
-640.9 -642.2
1351.9 1350.3
-2352.0 -2352.3
-135.5 -115.3
1225.7 1225.8
245.0 245.0
582.6 581.7
-538.8 -538.7
907.9 907.4
813.9 813.7
304.4 283.5
120.9 120.5
-189.0 -188.4
-335.3 -334.9
180.7 180.9
70.7 70.4
-329.0 -329.2
-233.0 -232.9
359.9 360.1
23.9 47.0
192.4 192.3
196.8 197.0
-141.0 -140.9
-119.1 -119.1
-157.5 -157.4
15.7 16.0
3.9 4.3
100.1 100.1
69.5 69.5
68.0 67.6
4.3 -20.6
72.9 72.8
33.5 33.3
-130.0 -129.8
58.9 58.7
-28.9 -28.9
-66.6 -66.6
13.2 13.1
7.3 7.3
-71.0 -70.8
62.4 62.4
81.4 81.3
-76.1 -76.0
-81.8 -54.3
-6.7 -6.8
-19.6 -19.5
51.7 51.8
5.6 5.6
15.1 15.1
24.5 24.4
9.4 9.3
3.3 3.3
-2.8 -2.9
-27.5 -27.5
6.6 6.6
-2.3 -2.3
24.2 24.0
9.1 8.9
39.4 10.0
-16.7 -16.8
-18.3 -18.3
-3.2 -3.2
13.2 13.2
-20.5 -20.6
-14.7 -14.6
13.3 13.3
16.2 16.2
11.8 11.8
5.7 5.7
-15.9 -16.0
-9.2 -9.1
-2.0 -2.0
2.2 2.3
5.4 5.3
8.7 8.8
-53.8 -21.8
3.0 3.0
10.7 10.8
-3.4 -3.2
11.8 11.7
0.7 0.7
-6.8 -6.7
-13.2 -13.2
-6.9 -6.9
-0.2 -0.1
7.7 7.8
8.7 8.7
1.1 1.0
-9.0 -9.1
-3.9 -3.9
-10.5 -10.5
8.4 8.4
-2.0 -2.0
-6.0 -6.3
37.6 3.3
0.2 0.2
-0.3 -0.4
0.5 0.6
4.5 4.5
-0.5 -0.6
4.4 4.4
1.7 1.7
-7.9 -7.9
-0.6 -0.7
-0.6 -0.6
2.2 2.1
-4.2 -4.2
2.4 2.3
-2.8 -2.9
-1.8 -1.8
-1.1 -1.1
-3.6 -3.6
-8.7 -8.7
3.0 3.0
-1.5 -1.4
-37.5 0.0
-2.3 -2.3
2.1 2.1
2.0 2.1
-0.6 -0.6
-0.8 -0.8
-1.0 -1.1
0.6 0.6
0.7 0.8
-0.8 -0.7
-0.3 -0.2
0.2 0.1
-2.1 -2.1
1.7 1.7
-1.4 -1.4
-0.2 -0.2
-2.5 -2.6
0.4 0.4
-2.0 -2.0
3.5 3.5
-2.3 -2.3
-2.1 -2.1
0.1 -0.2
38.8 -1.1
0.5 0.5
0.5 0.4
1.2 1.2
1.7 1.8
-0.9 -0.9
-2.2 -2.2
0.9 0.8
0.2 0.3
0.2 0.1
0.7 0.7
0.5 0.5
-0.1 -0.1
-0.3 -0.4
0.3 0.3
-0.5 -0.4
0.2 0.2
0.2 0.2
-0.9 -0.9
-0.9 -0.9
-0.2 -0.2
0.0 -0.0
0.7 0.7
-0.0 -0.0
-1.0 -0.9
-44.6 -0.9
0.4 0.4
0.4 0.5
0.6 0.6
1.6 1.6
-0.5 -0.4
-0.5 -0.5
1.0 1.0
-1.3 -1.2
-0.4 -0.2
-0.2 -0.1
0.9 0.8
0.4 0.4
-0.2 -0.1
-0.0 -0.0
0.4 0.4
0.5 0.5
0.0 0.1
0.5 0.5
0.5 0.5
-0.3 -0.3
-0.3 -0.3
-0.4 -0.4
-0.3 -0.4
-0.7 -0.7
Exercise#
Above we took a simple approach and computed a model for 2015.0 uding VO data for 2015.0. Use VOs to produce a model at a time of your choice between 2014 and 2018 (other than 2015.0 as we did above) and compare your coefficients to the IGRF at that time. Hints: For dates other than yyyy.0, you will need to interpolate the IGRF coefficients.
Exercise#
Create a second spherical harmonic model based on ground observatory data only and compare it to your satellite data only model and to the IGRF. To do this, you can use observatory annual means as the input data, which we have supplied in the file oamjumpsapplied.dat in the external data directory. Hint: The mag module contains a function that will extract all annual mean values for all observatories in a given year.
# Install pooch (not currently in VRE)
import sys
!{sys.executable} -m pip install pooch
Requirement already satisfied: pooch in /opt/conda/lib/python3.9/site-packages (1.7.0)
Requirement already satisfied: requests>=2.19.0 in /opt/conda/lib/python3.9/site-packages (from pooch) (2.27.1)
Requirement already satisfied: packaging>=20.0 in /opt/conda/lib/python3.9/site-packages (from pooch) (21.3)
Requirement already satisfied: platformdirs>=2.5.0 in /opt/conda/lib/python3.9/site-packages (from pooch) (2.5.0)
Requirement already satisfied: pyparsing!=3.0.5,>=2.0.2 in /opt/conda/lib/python3.9/site-packages (from packaging>=20.0->pooch) (3.0.7)
Requirement already satisfied: certifi>=2017.4.17 in /opt/conda/lib/python3.9/site-packages (from requests>=2.19.0->pooch) (2021.10.8)
Requirement already satisfied: charset-normalizer~=2.0.0 in /opt/conda/lib/python3.9/site-packages (from requests>=2.19.0->pooch) (2.0.12)
Requirement already satisfied: idna<4,>=2.5 in /opt/conda/lib/python3.9/site-packages (from requests>=2.19.0->pooch) (3.3)
Requirement already satisfied: urllib3<1.27,>=1.21.1 in /opt/conda/lib/python3.9/site-packages (from requests>=2.19.0->pooch) (1.26.8)
WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv
[notice] A new release of pip is available: 23.0.1 -> 23.1.2
[notice] To update, run: pip install --upgrade pip
# Fetch the data and import the relevant function
import pooch
oamjumpsapplied = pooch.retrieve(
"https://raw.githubusercontent.com/MagneticEarth/IAGA_SummerSchool2019/master/data/external/oamjumpsapplied.dat",
known_hash="dee77ded79cb0d86e3366a550830cad9de741322212faf9a74f3d03cb6bdd872"
)
from src.mag import obs_ann_means_one_year
Downloading data from 'https://raw.githubusercontent.com/MagneticEarth/IAGA_SummerSchool2019/master/data/external/oamjumpsapplied.dat' to file '/home/jovyan/.cache/pooch/c1a0acda735b5c4d0b60def6e59ddb56-oamjumpsapplied.dat'.
input_data = obs_ann_means_one_year(2000, oamjumpsapplied)
input_data
| Code | Colat | Long | alt(m) | year | D | I | H | X | Y | Z | F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ALE | 7.500 | 297.650 | 60 | 2000.5 | -67.510 | 86.448 | 3448 | 1319 | -3186 | 55553 | 55660 |
| 2 | NAL | 11.083 | 11.933 | 12 | 2000.5 | 0.332 | 82.317 | 7263 | 7263 | 42 | 53841 | 54329 |
| 3 | CCS | 12.283 | 104.283 | 10 | 2000.5 | 14.762 | 87.143 | 2929 | 2832 | 746 | 58709 | 58781 |
| 4 | THL | 12.517 | 290.833 | 57 | 2000.5 | -63.167 | 86.060 | 3877 | 1750 | -3460 | 56298 | 56431 |
| 5 | HRN | 13.000 | 15.550 | 15 | 2000.5 | 2.925 | 81.500 | 7996 | 7986 | 408 | 53504 | 54098 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 196 | SYO | 159.000 | 39.583 | 0 | 2000.6 | -48.527 | -63.777 | 19168 | 12694 | -14362 | -38913 | 43378 |
| 197 | VNA | 160.650 | 351.750 | 40 | 2000.5 | -12.907 | -61.207 | 18977 | 18498 | -4239 | -34529 | 39400 |
| 198 | TNB | 164.683 | 164.117 | 28 | 2000.0 | 136.233 | -83.013 | 7829 | -5654 | 5415 | -63886 | 64364 |
| 199 | SBA | 167.850 | 166.783 | 10 | 2000.5 | 155.260 | -80.390 | 11212 | -10183 | 4692 | -66219 | 67161 |
| 200 | VOS | 168.450 | 106.867 | 3500 | 2000.5 | -120.678 | -76.992 | 13443 | -6859 | -11562 | -58192 | 59725 |
200 rows × 12 columns
Acknowledgements#
The land/sea data file was provided by John Stevenson (BGS). The VO data were computed by Magnus Hammer (DTU) and the file prepared by Will Brown (BGS).